数据挖掘之特征工程
1、 什么是特征工程
特征工程最主要的是通过专业背景知识和技巧处理数据,改善特征或者构建新的特征,使其能在机器学习算法上发挥更好的作用的过程。
在数据建模时,如果对原始数据的所有属性进行学习,并不能很好的找到数据的潜在趋势,而通过特征工程,算法模型能够减少噪声的干扰,这样能够更好的找出数据趋势。优秀的特征甚至能够帮你实现使用简单的模型达到很好的效果。可以说,数据和特征决定了整个模型效果的上限,而改进算法只是在逼近这个上限。
2、 简单特征构造方法
2.1、类别编码
数据中经常会遇到一些地区、国家、性别等字符信息,需要将其通过特定的编码方式转化为数值型数据,常见的编码方式有one_hot编码,label_encoder编码。
- label_encoder编码
label_encoder会将不同字符编码为整数,例如,如果某列含有8个不同的字符,则label_encoder会将其编码为0到8的整数集合。
from sklearn.preprocessing import LabelEncoder
data[category_fea] = LabelEncoder().fit_transform(data[fea])
- one-hot编码
one-hot编码,又称为一位有效编码,主要是采用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候只有一位有效。
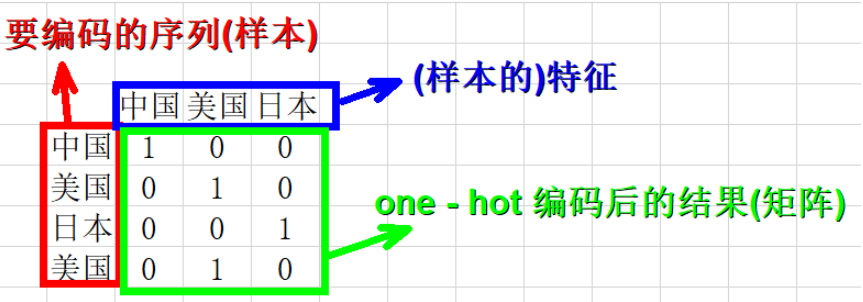
例如,将一列数据:["中国", "美国", "日本", "美国"],进行one-hot编码。其结果如上图所示。
from sklearn.preprocessing import OneHotEncoder
data[onehot_fea] = OneHotEncoder().fit_transform(data[fea])
2.2、非线性变换特征
非线性变换包括对数转换、平方根转换、平方转换、幂转换等。
import numpy as np
data['log'] = np.log(data[fea])
data['sqrt'] = np.sqrt(data[fea])
data['square'] = np.square(data[fea])
2.3、离散化特征
特征离散化就是把连续特征分段,每一段内的原始连续特征无差别的看成同一个新特征。离散化的特征更易于理解、可以简化模型,提高模型准确度,提高运行速度。
2.4、统计特征
- 连续数据统计特征,如最大值、最小值、平均值、方差、累加和等
使用时,通常先对数据进行分组后,再逐一计算统计特征,例如按国家分组后,计算每组每年增长人口的最大值、最小值、平均值、方差等。
feature['max'] = data.groupby(groupfea)[fea].max()
feature['min'] = data.groupby(groupfea)[fea].min()
feature['mean'] = data.groupby(groupfea)[fea].mean()
feature['std'] = data.groupby(groupfea)[fea].std()
feature['sum'] = data.groupby(groupfea)[fea].sum()
- 离散数据统计特征,如众数、熵、计数等
使用时,也是先对数据进行分组后,再逐一计算统计特征。
from scipy.stats import entropy
feature['mode'] = data.groupby(groupfea)[fea].agg(lambda x: x.mode())
feature[entropy'] = data.groupby(groupfea)[fea].transform(lambda x: entropy(x.value_counts() / x.shape[0])